核密度估计(Kernel density estimation, KDE)是统计学中一种常见的对于概率密度函数(Probability density function, pdf)的非参数(non-parametric)估计。
要搞清楚什么是 KDE,首先需要明白什么是核(Kernel)。
核函数 Kernel
在信号处理中,窗函数(Window function)被广泛使用。窗函数是一个在指定区间外取值为零的函数,并且通常在中心处取得峰值并围绕中心左右对称。当核函数乘到原始波形的函数中时,区间外的信号归零,只有区间内的信号被留下(并可能发生一些变换以凸显特征),就像透过一扇窗户看一样。最简单的窗函数之一便是区间内为1区间外为0的函数,相当于直接将区间内的信号取出。
在统计学中,核函数(Kernel function)的概念对应于信号处理领域的窗函数。在统计学的不同分支下,核函数有着不同的具体定义。
贝叶斯统计学 Bayesian Statistics
在贝叶斯统计学中,核函数指函数的 pdf 中包含自变量的那一部分。比如正态分布,它的 pdf 是
\[p(x|\mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\]这里 $x$ 是唯一的自变量,pdf 的前一部分不包含 $x$ 因而被丢掉,正态分布的核具有以下形式
\[p(x|\mu ,\sigma ^{2})\propto e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\]模式识别领域 Pattern Recognition
在模式识别领域,核函数被广泛使用,比如支持向量机等方法就会用到。关于模式识别领域(或更广义上的机器学习领域)的核函数,知乎上有一些比较好的回答。
非参数统计学 Non-parametric Statistics
非参数统计学是统计学的一个重要分支。我们一般学习的统计学中,所有的工作(统计推断、检验等等)围绕一个特定分布中的参数展开(常见的参数如控制位置的参数 均值 $\mu$、控制形状的参数 方差 $\sigma$ 等)。而非参数统计与此相反。
非参数统计学中的核函数是一个非负、可积的实函数 $K$。此外,在实际使用中还需满足以下两个条件:
-
归一性 Normalization
\[\int _{-\infty }^{+\infty }K(u)\,du=1\,;\] -
对称性 Symmetry
\[K(-u)=K(u){\mbox{ for all values of }}u\,.\]
核密度估计 KDE
令 $(x_1, x_2, …, x_n)$ 组成独立同分布(independent and identically distributed, iid)的一个样本(Sample),而该分布的密度函数 $f$ 未知。我需要从样本中有限的数据来估计 $f$。核密度估计函数(Kernel density estimator)定义为
\[{\displaystyle {\widehat {f}}_{h}(x)={\frac {1}{n}}\sum _{i=1}^{n}K_{h}(x-x_{i})={\frac {1}{nh}}\sum _{i=1}^{n}K{\Big (}{\frac {x-x_{i}}{h}}{\Big )},}\]($K$:核函数,$h>0$:带宽,一个控制平滑程度的参数)
例子
假设我们得到的样本数据如下:
| Sample No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Value | -2.1 | -1.3 | -0.4 | 1.9 | 5.1 | 6.2 |
可以画出一个简单的直方图:
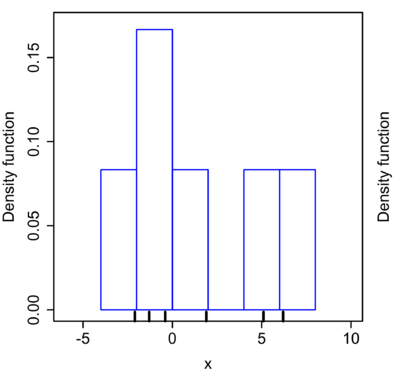
而运用核密度估计的方法,选用正态核,在每个数据点上放置一个 $\sigma=2.25$ 的正态核函数(红线),将红线相加即得到核密度估计值(Kernel density estimate,蓝线)。
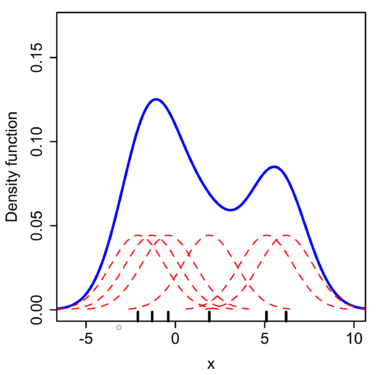
可以看到,相比直方图,KDE 得到的曲线更加平滑。在实际操作中,随着样本数据量的增加,KDE 也比直方图更快收敛于真实的密度曲线。